MAKALAH SISTEM BERBASIS PENGETAHUAN
METODE INFERENSI
DISUSUN OLEH :
ARGA PRATAMA RIZKY
1B116196
3 KA 24
UNIVERSITAS GUNADARMA
JAKARTA
2017
KATA PENGANTAR
Puji syukur kami ucapkan
kehadirat Allah SWT, yang telah memberikan Rahmat dan HidayahNya, sehingga
penyusun dapat menyelesaikan makalah yang berjudul “Metode Inferensi”. Makalah
ini dibuat dengan tujuan untuk menambah pengetahuan penyusun dan untuk memenuhi
tugas mata kuliah Sistem Berbasis Pengetahuan. Demi kesempurnaan makalah ini,
penyusun mohon kritik dan saran dari pembaca yang bersifat membangun.
Demikianlah makalah ini saya buat
semoga dapat bermanfaat bagi para pembaca semua, apabila ada kekurangan mohon
maaf sebesar-besarnya.
Bekasi, 21 November 2017
Hormat
Kami,
Penyusun
1.
Trees, Lattice
dan Graph
Tree (pohon)
adalah suatu hierarki struktur yang terdiri dari Node (simpul/veteks) yang menyimpan informasi atau pengetahuan dan
cabang (link/edge) yang menghubungkan node. Binary tree mempunyai 0,1 atau 2
cabang per-node.
·
Node tertinggi disebut root
·
Node terendah disebut daun
Tree merupakan tipe khusus dari
jaringan semantic, yang setiap nodenya kecuali akar, mempunyai satu node orang
tua dan mempunyai nol atau lebih node anak. Tree adalah kasus khusus dalam
Graph. Graph dapat mempunyai nol atau lebih link di antara node dan tidak ada
perbedaan antara orangtua dan anak.
Dalam graph, link dapat ditunjukkan berupa panah atau arah yang memadukan node dan bobot yang merupakan karakteristik beberapa aspek dari link.
Dalam graph, link dapat ditunjukkan berupa panah atau arah yang memadukan node dan bobot yang merupakan karakteristik beberapa aspek dari link.
Note :
– Graph asiklik adalah graph yang tidak mengandung siklus.
– Graph dengan link berarah disebut digraph.
– Graph asiklik berarah disebut lattice.
– Tree yang hanya dengan path tunggal dari akar untuk satu daun disebut degeneratetree.
– Aplikasi tree dan lattice adalah pembuatan keputusan disebut decision tree dan decision lattice.
– Contoh : decision tree yang menunjukkan pengetahuan tentang hewan.
– Graph asiklik adalah graph yang tidak mengandung siklus.
– Graph dengan link berarah disebut digraph.
– Graph asiklik berarah disebut lattice.
– Tree yang hanya dengan path tunggal dari akar untuk satu daun disebut degeneratetree.
– Aplikasi tree dan lattice adalah pembuatan keputusan disebut decision tree dan decision lattice.
– Contoh : decision tree yang menunjukkan pengetahuan tentang hewan.
– Aturan produksi (IF…THEN…) dari contoh di atas :
JIKA pertanyaan=”Apakah dia bertubuh besar ?”
DAN jawaban=”Tidak”
MAKA pertanyaan=”Apakah dia mencicit?”
JIKA pertanyaan=”Apakah dia bertubuh besar ?”
DAN jawaban=”Tidak”
MAKA pertanyaan=”Apakah dia mencicit?”
JIKA pertanyaan=”Apakah dia bertubuh besar ?”
DAN jawaban=”Ya”
MAKA pertanyaan=”Apakah dia mempunyai leher panjang?”
dst……
DAN jawaban=”Ya”
MAKA pertanyaan=”Apakah dia mempunyai leher panjang?”
dst……
2.
Spasi
Stata dan Spasi Permasalahan
a) State Space
State adalah kumpulan
karakteristik yg dapat digunakan untuk menentukan status. State Space adalah
rangkaian pernyataan yg menunjukkan transisi antara state dimana objek
dieksprerimen.
3.
AND-OR Tree
dan Goals
Dalam SP, untuk menemukan solusi problem dapat
menggunakan rangkaian backward yaitu dengan tree AND-OR dan AND-OR-NOT.
·
Banyak tipe system pakar menggunakan backward chaining untuk mendapatkan
solusi dari permasalahan.
·
Salah satu tipe dari tree atau lattice yang
digunakan dalam masalah representasi backward
chaining adalah Pohon AND-OR.
Contoh :
LULUS Sid.Sarjana
|
Persyaratan
|
SKS =160
IPK >=2.0
|
Lulus
|
KURSUS
|
WORKSHOP
|
LULUS D3
|
4.
Logika
Deduktif dan Syllogisme
Tipe-tipe Inferensi, yaitu :
a) Deduction
Pemberian
alasan logikal dimana kesimpulan harus mengikuti premis
b)
Induction
Inferensi
dari khusus ke umum
c) Intuition
Tidak ada
teori yg menjamin. Jawabannya hanya muncul, mungkin dengan penentuan pola yg
ada secara tidak disadari.
d) Heuristic
Aturan yg
didasarkan pada pengalaman
e) Generate & Test
Trial dan
error. Digunakan dgn perencanaan.
f) Abduction
Pemberian
alasan kembali dari kesimpulan yg benar ke premis .
g) Default
Diasumsikan
pengetahuan umum sebagai default
h)
Autoepistemic
Self-knowledge
i)
Nonmonotonic
Pengetahuan
yg sebelumnya mungkin tdk benar jika bukti baru didapatkan
j)
Analogy
Kesimpulan yg berdasarkan pada
persamaan untuk situasi yg lainnya.
Suatu logika argument adalah
kumpulan dari pernyataan-pernyataan yang dinyatakan untuk dibenarkan sebagai
dasar dari rantai penalaran. Salah satu jenis logika argunen adalah Silogisme. Penalaran deduktif umumnya
terdiri dari tiga bagian : premis mayor,
premis minor dan konklusi. Premis
disebut juga antecedent Konklusi/kesimpulan
disebut juga consequent. Silogisme
dapat direpresentasikan ke dalam bentuk aturan JIKA…..MAKA….. (IF…THEN…..),
Contoh :
JIKA siapapun yang dapat membuat Robot adalah pintar
DAN Jono dapat membuat robot
MAKA Jono adalah pintar
Silogisme klasik disebut categoricall syllogism (silogisme yang
pasti). Premis dan konklusi didefinisikan sebagai statement yang pasti dari
empat bentuk berikut :
Bentuk
|
Skema
|
Arti
|
A
|
Semua S adalah P
|
Universal Afirmative
|
E
|
Tidak S adalah P
|
Universal Negative
|
I
|
Beberapa S adalah P
|
Particular Afirmative
|
O
|
Beberapa S bukan P
|
ParticularNegative
|
Subjek dari konklusi S disebut
bagian minor bila predikat konklusi P adalah bagian mayor. Premis terdiri dari
premis mayor dan premis minor.
Contoh :
Premis mayor : Semua
M adalah P
Premis minor : Semua S adalah M
Konklusi : Semua S adalah P
Silogisme di atas adalah bentuk
standar karena premis mayor dan minor sudah diketahui.
Contoh :
“Semua mikrokomputer adalah
computer”
Subjeknya (objek yang
digambarkan) adalah mikrokomputer.
Predikatnya (beberapa sifat
subjek) adalah computer
M (middle term) adalah hal yang penting karena
silogisme didefinisikan sedemikian sehingga konklusi tidak dapat disimpulkan
dengan mengambil salah satu premis. Q (quantifier) menggambarkan porsi dari
kelas yang diketahui. Quantifier
“semua” dan “tidak” adalah universal karean menunjukkan keseluruhan kelas. “beberapa” adalah khusus
(particular) karena hanya menunjukkan satu bagian dari kelas yang diketahui.
Mood dari silogisme didefinisikan sebagai tiga
huruf yang memberikan bentuk masing-masing premis mayor, minor dan konklusi.
Contoh :
Semua
M adalah P
Semua
S adalah M
\Semua S
adalah P
menunjukkan suatu mood AAA-1
Ada 4 kemungkinan pola susunan istilah S, P dan M :
Figure 1
|
Figure 2
|
Figure 3
|
Figure 4
|
|
Premis Mayor
|
MP
|
PM
|
MP
|
PM
|
Premis Minor
|
SM
|
SM
|
MS
|
MS
|
Tidak selalu argument yang mempunyai bentuk
silogisme merupakan silogisme yang valid.
Contoh : Silogisme tidak valid berbentuk AEE-1
Semua M adalah P
Tidak S adalah M
\Tidak S
adalah P
Semua mikrokomputer adalah computer
Bukan mainframe adalah mikrokomputer
\Bukan
mainframe adalah computer
Diperlukan prosedur keputusan (decision procedure) untuk pembuktian validitas. Prosedur keputusan
untuk silogisme dapat dilakukan menggunakan diagram venn tiga lingkaran yang
saling berpotongan yang merepresentasikan S,P, M.
Contoh : Prosedur Keputusan untuk AEE-1
Semua M adalah P
Tidak S adalah M
\Tidak S
adalah P
a. Diagram Venn b. Setelah Premis Mayor c. Setelah Premis Minor
|
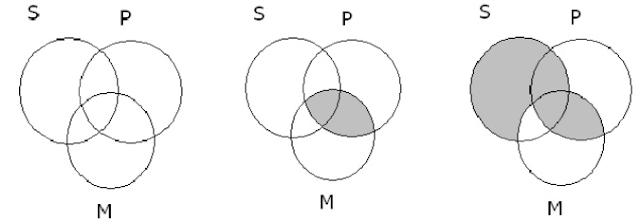
Contoh : Prosedur Keputusan untuk EAE-1
Tidak M adalah P
Semua
S adalah M
\Tidak S
adalah P
a. Diagram Venn b. Setelah Premis Mayor c. Setelah Premis Minor
|
5.
Resolusi,
Sistem Resolusi dan Deduksi
Refutation adalah pembuktian teorema dengan
menunjukkan negasi atau pembuktian kontradiksi melalui reductio ad absurdum.
Melakukan refute berarti membuktikan kesalahan.
Contoh :
A à B
B à C
C à D
\A à D
Untuk membuktikan konklusi A à D adalah suatu teorema melalui resolusi
refutation, hal yang dilakukan :
p à q º ~p Ú q
sehingga
Aà D º ~A Ú D
dan langkah terakhir adalah melakukan negasi
~(~A
Ú D) º A Ù ~D
Penggunaan konjungsi dari
disjunctive form pada premis dan negasi pada konsklusi, memberikan conjuctive
normal form yang cocok untuk resolusi refutation.
Dari contoh di atas, penulisannya menjadi :
Akar bernilai nill, menunjukkan kontradiksi.
Sehingga melalui refutation dapat ditunjukkan konklusi asli (awal) adalah teorema dengan peran kontradiksi.
6.
Shallow
dan Casual Reasoning
Sistem pakar menggunakan rantai
inferensi, dimana rantai yang panjang merepresentasikan lebih banyak causal
atau pengetahuan yang mendalam. Sedangkan shallow umumnya menggunakan kaidah
tunggal atau inferensi yang sedikit.
Kualitas inferensi juga faktor
utama dalam penentuan kedalaman dan pendangkalan dari penalaran. Shallow knowledge disebut juga experiment
knowledge.
Contoh : Penalaran shallow
IF a car has
a
good battery
good
sparkplugs {conditional elements}
gas
good
tires
THEN the car can move
Pada penalaran shallow, tidak ada atau hanya
terdapat sedikit pemahaman dari subjek, dikarenakan tidak ada atau hanya
terdapat sedikit rantai inferensi.
Keuntungan dari penalaran shallow :
a) Kemudahan
dalam pemograman, yang berarti waktu pengembangan program menjadi singkat,
b) Program
menjadi lebih kecil,
c) Lebih
cepat
d) Biaya
pengembangan menjadi murah.
7. Forward Chaining dan Backward Chaining
Chain (rantai) : perkalian inferensi yang
menghubung-kan suatu permasalahan dengan solusinya.
Forward
chaining :
·
Suatu rantai yang dicari atau dilewati/dilintasi
dari suatu permasalahan untuk memperoleh solusi.
·
Penalaran dari fakta menuju konklusi yang terdapat
dari fakta.
Backward
chaining :
·
Suatu rantai yang dilintasi dari suatu hipotesa
kembali ke fakta yang mendukung hipotesa tersebut.
·
Tujuan yang dapat dipenuhi dengan pemenuhan sub
tujuannya.
Contoh rantai inferensi :
gajah(x) à mamalia
(x)
mamalia(x) à
binatang(x)
·
Causal
(sebab-akibat) Forward chain
gajah(clyde)
⎹
gajah(x) → mamalia(x)
⎹
⎹
gajah(x) → mamalia(x)
⎹
mamalia(x) → binatang(x)
⎹
⎹
binatang(clyde)
·
Explicit
Causal chain
gajah(clyde)
unifikasi ⎹
implikasi gajah(clyde) → mamalia(clyde)
unifikasi ⎹
implikasi mamalia(clyde) →
Karakteristik
Forward dan Backward chaining
Forward
chaining
|
Backward
chaining
|
Perencanaan, monitoring, kontrol
|
Diagnosis
|
Disajkan untuk masa depan
|
Disajikan untuk masa lalu
|
Antecedent ke konsekuen
|
Konsekuen ke antecedent
|
Data memandu, penalaran dari bawah ke atas
|
Tujuan memandu, penalaran dari atas ke bawah
|
Bekerja ke depan untuk mendapatkan solusi apa
yang mengikuti fakta
|
Bekerja ke belakang untuk mendapatkan fakta yang
mendukung hipotesis
|
Breadth
first search dimudahkan
|
Depth
first search dimudahkan
|
Antecedent
menentukan pencarian
|
Konsekuen
menentukan pencarian
|
Penjelasan tidak difasilitasi
|
Penjelasan difasilitasi
|
https://www.scribd.com/doc/42183339/Sistem-Berbasis-Pengetahuan-Metode-Inferensi
http://panjipurnama28.blogspot.co.id/2016/01/metode-inferensi.html